算法
- 定義:即工具,如何恰當使用這些工具
- 單變量線性回歸算法
- 線性:
- 判斷方法:所有未知數的冪次項為一次
- 線性方程式舉例:
- x+7=6, x為未知數, 冪次為1
- {x+y=4,x-2y=7} , x,y 為未知數, 冪次為1
- 非線性方程式舉例:
- x^2+3x+4=0, x為未知數, 冪次為2
- sin(x)+x=4, x為未知數, 出現在超越函數內
- 線性回歸: 是在資料點中找出規律、畫出一條直線的專業說法
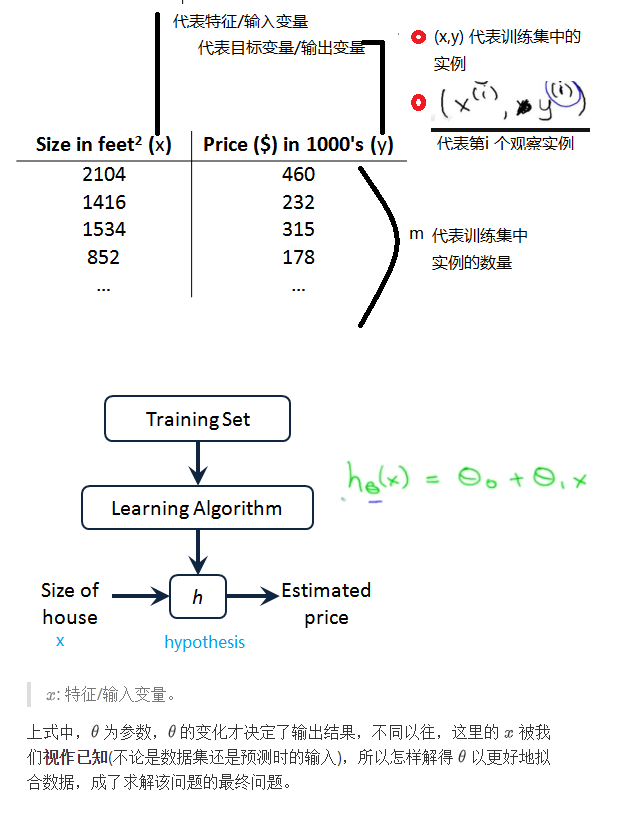
- 模型
- 代價函數(cost function)
- 代價函數越小,就代表了模型對訓練數據擬合的越好。即最優化經驗風險
- 定義:計算整個訓練集所有損失函數之和的平均值
- 損失函數(Loss/Error function)定義:計算單個訓練集之誤差
- 低度下降(gradient descent)
- 線性代數複習
% 1.Matrices and Vectors
A = [1, 2, 3; 4, 5, 6; 7, 8, 9; 10, 11, 12]
v = [1;2;3]
[m,n] = size(A)
dim_A = size(A)
dim_v = size(v)
A_23 = A(2,3)
% 2.Addition and Scalar Multiplication
A = [1, 2, 4; 5, 3, 2]
B = [1, 3, 4; 1, 1, 1]
s = 2
add_AB = A + B
sub_AB = A - B
mult_As = A * s
div_As = A / s
add_As = A + s
% 3.Matrix Vector Multiplication
A = [1, 2, 3; 4, 5, 6;7, 8, 9]
v = [1; 1; 1]
Av = A * v
% 4. Matrix Matrix Multiplication
A = [1, 2; 3, 4;5, 6]
B = [1; 2]
mult_AB = A*B
% 5.Matrix Multiplication Properties
A = [1,2;4,5]
B = [1,1;0,2]
% same as I = [1,0;0,1]. Initialize a 2 by 2 identity matrix
I = eye(2)
% IA=AI
IA=I*A
AI=A*I
% AB not equal BA
AB=A*B
BA=B*A
% 6. Inverse and Transpose
A = [1,2,0;0,5,6;7,0,9]
A_trans = A'
A =
1 2 0
0 5 6
7 0 9
A_trans =
1 0 7
2 5 0
0 6 9
% Take the inverse of A
A_inv = inv(A)
% What is A^(-1)*A?
A_invA = inv(A)*A

參考
